原理：

设归并排序的当前区间为R[low...high]，分治法的三个步骤是：

• 分解：将当前区间一分为二，即求分裂点
• 求解：递归地对两个子区间R[low...mid]和R[mid+1...high]进行归并排序
• 组合：将已排序的两个子区间R[low...mid]和R[mid+1...high]归并为一个有序的区间R[low...high]

递归的终结条件：子区间的长度为1

算法示意图：

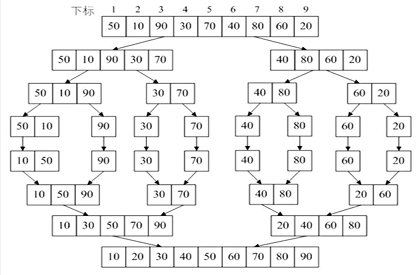
代码：

class Solution {
public:
    void merge(vector<int>& nums, int low, int high, vector<int>& result){
		int left_start = low, left_len = (high - low) / 2 + 1;
        int right_start = low + left_len;
        int cnt = low;
        while(left_start < low + left_len && right_start < high + 1){
            if(nums[left_start] < nums[right_start])	result[cnt++] = nums[left_start++];
            else	result[cnt++] = nums[right_start++];
        }
        while(left_start < low + left_len)	result[cnt++] = nums[left_start++];
        while(right_start < high + 1)	result[cnt++] = nums[right_start++];
    }
    
    void mergeSort(vector<int>& nums, int low, int high, vector<int>& result){
		if(low < high){
			int mid = (low + high) / 2;
            mergeSort(nums, low, mid, result);
            mergeSort(nums, mid+1, high, result);
            merge(nums, low, high, result);
            for(int i = low; i <= high; i++)	nums[i] = result[i];
        }
    }
};

复杂度分析：

• 时间复杂度：

最差时间复杂度： O(nlogn)

平均时间复杂度：O(nlogn)

• 空间复杂度：

最差空间复杂度：O(n)

稳定性：稳定