原理：

快速排序，即选定基准数据并找出其正确索引位置的过程。

通过使用分治思想对快速排序算法进行描述。下面对一个典型的子数组nums[p...r]进行快速排序的三步分治过程：

  分解：数组nums[p...r]被划分为两个（可能为空）子数组nums[p...q-1]和nums[q+1...r]，使得nums[p...q-1]中的每个元素都小于nums[q]，而nums[q+1...r]中的每个元素都大于nums[q]。

  解决：通过递归调用快速排序，对数组nums[p...q-1]和nums[q+1...r]进行排序。

  合并：因为子数组都是原址排序的，所以不需要合并操作：数组nums[p...r]已经有序。

下面以一个实例来描述快速排序的过程。

如下图所示，假设最开始的基准数据为数组第一个元素23，则首先用一个临时变量取存储基准数据，即tmp = 23；然后分别从数组的两端扫描数组，设两个指示标志：low指向起始位置，high指向末尾位置。

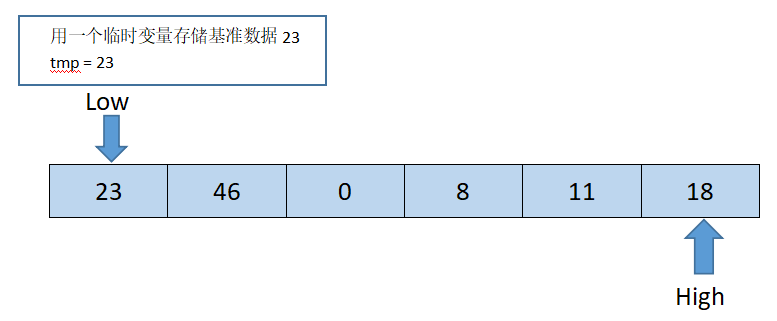
首先从后半部分开始比较，如果扫描到的值大于基准数据就让high-1，如果发现有元素比基准元素值小（如上图18<=tmp），就将high位置的值赋值给low位置。

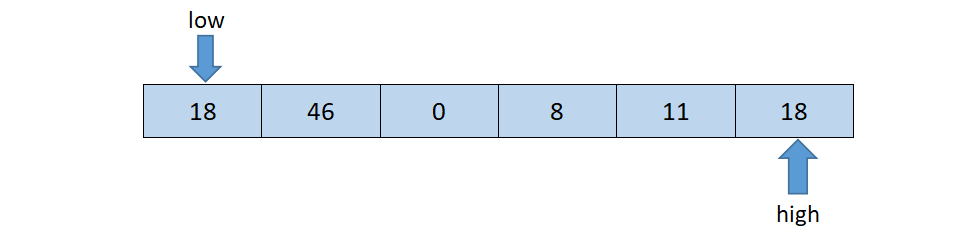
然后开始从前往后扫描，如果扫描到的元素小于基准元素，则low+1；如果发现有元素大于基准元素的值(如上图46 >= tmp)，就将low位置的值赋值给high位置。指针移动并且数据交换后的结果如下所示：

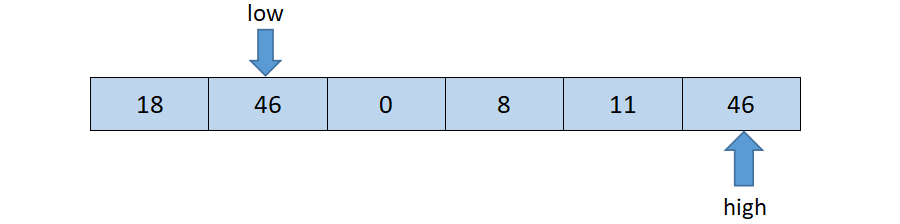
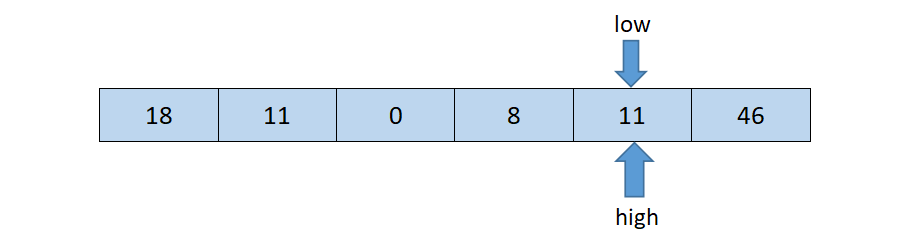
然后再开始从后往前扫描，原理同上，发现11 <= tmp，则将high位置的值赋给low位置，结果如下：

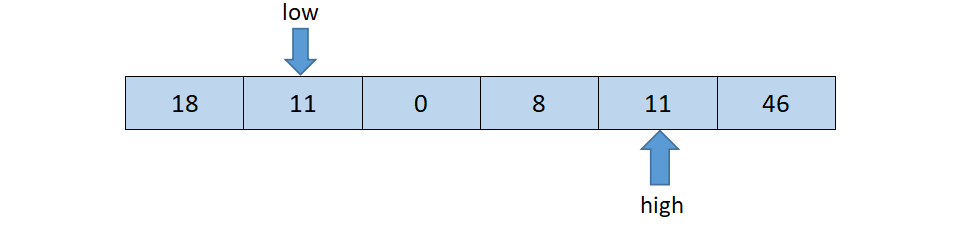
然后再从前往后扫描，直到low==high结束循环，此时low或者high的下标就是基准数据23在该数组中的正确索引位置，如下图所示：

这样一遍走下来，就可以确定一个元素的位置，以后采用递归的方式，分别对前半部分和后半部分排序。

几个要点：

• 确定基准元素后，先从high向前开始比较。
• 在遍历比较时，判断是否满足>=或<=，即等于时不用交换。
• 循环结束的条件为low>=high。循环结束后，需要将基准元素值写入当前的low或high位置。

代码：

class Solution {
public:
    int partition(vector<int>& nums, int low, int high){
        int tmp = nums[low];	// 设置基准数据
        while(low < high){
			while(low < high && nums[high] >= tmp)	high--;
            nums[low] = nums[high];
            while(low < high && nums[low] <= tmp)	low++;
            nums[high] = nums[low];
        }
        nums[low] = tmp;
        return low;
    }
    
    void quickSort(vector<int>& nums, int low, int high){
        if(low < high){
			int mid = partition(nums, low, high);
            quickSort(nums, low, mid-1);
            quickSort(nums, mid+1, high);
        }
    }
};

随机快速排序：

随机快排在确定基准元素时，采用一种随机抽样的随机化技术，使得从数组nums[l...r]中随机选取一个元素作为基准元素。由于基准元素的选取是随机的，舍得对输入数组的划分也是比较均衡的，从而获得较好的期望性能。

代码：

class Solution {
public:
    int partition(vector<int>& nums, int low, int high){
        int tmp = nums[low];
        while(low < high){
			while(low < high && nums[high] >= tmp)	high--;
            nums[low] = nums[high];
            while(low < high && nums[low] <= tmp)	low++;
            nums[high] = nums[low];
        }
        nums[low] = tmp;
        return low;
    }
    
    int random_partition(vector<int>& nums, int low, int high){
		int n = rand() % (high - low) + low;	// 随机选取下标
        swap(nums[low], nums[n]);	// 与low位置交换
        return partition(nums, low, high);
    }
    
    void quickSort(vector<int>& nums, int low, int high){
		if(low < high){
			int mid = random_partition(nums, low, high);
            quickSort(nums, low, mid-1);
            quickSort(nums, mid+1, high);
        }
    }
};

复杂度分析：

• 时间复杂度：

  考虑到最好情况，每次都是均匀划分，则时间复杂度为O(nlgn)。

  但如果是最坏情况，比如[1,2,3,4,5]，复杂度变为O(n^2)。

• 空间复杂度：

  这里分析就地快速排序的空间复杂度。首先就地快速排序使用的空间是O(1)的，也就是常数级；而真正消耗空间的就是递归调用了，因为每次递归就要保持一些数据。

  最优的情况下空间复杂度为：O(logn)；每一次都平分数组的情况。

  最差的情况下空间复杂度为：O(n)；退化为冒泡排序的情况。